Solution for part 3 of homework #1

2.5

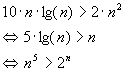
Let:

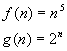
f and g are two strictly increasing functions (for n >0) and they have no inflexion point (the second order derivative never equals 0 for n>0), which means they have 0, 1 or 2 intersection points. On a plot of the two functions, one can see that they have two intersection points. We don’t need the exact values since n is an integer. From the graph, we conclude that f(n) > g(n) when: 1< n < 23.

From the equivalence relation shown above:

holds when 1< n < 23.

2.23

1^st method:

2^nd method:

It is a known result that: when

It is true in particular when

because O( ) notation allows multiplication

3^rd method

Let:

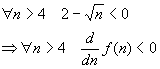
Therefore, for values of n superior to 4, the function f is decreasing. On top of that:

We can conclude:

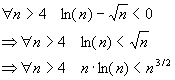
What we have proved by the last relation is exactly:

(above we have n0 = 4 and c =1)

2.29

Nothing can be said about the relative performance of the two algorithms. O(n^3) could mean n^1/2 as well as n^3.

2.1-4

1^st method:

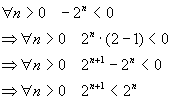
We have proved here that:

n0 = 0 and c= 1

2^nd method:

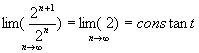
1^st method:

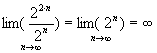
2^nd method:

Suppose I have n0 and c such that:

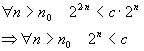
This last proposition doesn't make sense, so the supposition must be false.