Solution for the morning midterm

1. Complexity

Note: This is FAR more than was needed to get full credit on this problem. We just wanted to be as complete as possible!

a. Give the formal definition of big-O and big-theta

b. Prove or disprove that for any three functions f(x), g(x) and s(x): s(x)=O(f(x)) and s(x)=O(g(x)) imply s(x) = O((max(f(x), g(x))), but does not imply max(f(x), g(x)) = O(s(x))

* Suppose: and

(1)

(2)

(1) and (2) imply that we can introduce the two real numbers C₁ and C₂ and the two integers n₁ and n₂ such that:

(3)

(4)

Let:

and

Then from (3) and (4), we have:

(5)

(6)

Let k be a natural integer, we have two different cases:

In this case:

(7)

So, (5) implies that:

In this case:

(8)

So, (6) implies that:

(9)

In both cases (9) holds. As this was shown for any k, we can write:

Which implies that:

Which basically means:

This is what we wanted to prove.

Now suppose again: and

Consider these specific functions s, f and g:

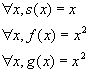
Note that:

These functions respect the hypothesis, but the following relation does not hold:

Therefore s(x)=O(f(x)) and s(x)=O(g(x)) does not imply max(f(x), g(x)) = O(s(x)).

c. Consider and prove or disprove these two statements:

h(x)=O(k(x)) and k(x)=O(h(x))

Let’s prove that h(x)=O(k(x))

We know:

(1)

(2)

(3)

We have:

(4)

On the other hand, we have:

(5)

Because the two functions and take only positive values when x is positive, (5) implies that:

(6)

Now:

Let’s prove that k(x)=O(h(x)) is not implied:

Suppose k(x) = O(h(x)):

Then:

Let C₁ and n₁ be such constants:

(1)

But it is easy to show that:

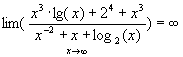(2)

(1) and (2)are incompatible, so our supposition was wrong. The statement k(x) = O(h(x)) is false.

Note: the formal reason why (1) and (2) are not compatible is the definition of the limit:

2. Search

15 pts: You are given two sorted arrays of distinct integers, a[] and b[]. There are N elements in a[] and M elments in b[], where M is equal to the square root of N. (Typical values might be N=1000000, M=1000)
Implement the function
int match(int a[], int b[], int N, int M); which has a return value of the number of elements found in both a and b. Your goal is to achive as low as asymtotic bound as possible. You may not use the STL for this problem.
```
// The following code does a binary search on A[] for 
// Each element in B
int match(int A[], int B[],int N, int M)
{
	int j;
	int count=0;

	for(j=0;j<M;j++)
		count+=bsearch(A,N,B[j]);	
	return count;
}

int bsearch(int A[],int N,int what)
{
	int r=N, l=0;
	int c;
    while (r >= l)
    { 
	    c=(l+r)/2;
	    if (what == A[c]) 
			return 1;
	    if (what < A[c]) 
			r = c-1; 
		else 
			l = c+1;
	}
	return 0;
}
```
5 pts: Give the tightest possible big-O complexity estimate for your program in terms of N then explain your answer.
Complexity is O(N^1/2*lg(N)). The reason is that we perform M binary searches. Each binary search takes O(lg(N)) time. And M is equal to the square root of N.
5 pts: If M were just as large as N would you use the same algorithm? Justify your answer. If you use a different algorthm, provide its tightest possible big-O complexity.
I'd use a different algorithm. Specifically I'd take the intersection of A and B as was done in the homework. This is O(N). The algorithm from part a would actually run in O(N*lg(N)) time if M=N.

3. Sorted Lists

Write a function which takes two sorted, NULL-terminated, linked lists as arguments. You are to return a pointer to a sorted, NULL-terminated, linked list which is a merge of the two lists. You must not change either of the two linked lists passed in.

#include <string.h> // for strcmp

// Client structure, with addition of "next" pointer
struct Client
{
	char f_name [40]; // first name
	char l_name [40]; // last name
	double money; // how much money do they have?
	Client * next; // pointer to next node
};

/*	operator<
	Returns true if client a is less than client b in lexicographic order.
*/
bool operator< (const Client & a, const Client & b)
{
	if (strcmp (a.l_name, b.l_name) < 0)
		return true;
	if (strcmp (a.l_name, b.l_name) == 0) // if last names are the same
		if (strcmp (a.f_name, b.f_name) < 0)
			return true;
	return false;
} // operator<

/*	addToList
	A utility function to aid in constructing result list. Takes a pointer to an
	item to add and pointers to the head and tail of the result list, and adds the
	new item to the tail of the result list.
*/
void addToList (Client * newItemIter, Client * & resultHead, Client * & resultTail)
{
	Client * newNode = new (Client);
	
	*newNode = *newItemIter; // default assignment operator does most of the work
	newNode -> next = NULL;
	
	if (resultHead == NULL) // if result list was empty
	{
		resultHead = newNode;
		resultTail = newNode;
	}
	else
	{
		resultTail -> next = newNode;
		resultTail = newNode;
	}
} // addToList

/*	merge
	The main function.
*/
Client * merge (Client * oldlist, Client * newlist)
{
	Client * olditer = oldlist; // iterator for stepping through old list
	Client * newiter = newlist; // iterator for stepping through new list
	
	Client * resultHead = NULL; // the list we'll return
	Client * resultTail = NULL;
	
	while (olditer || newiter) // while at least one list not at end
	{
		if (!olditer) // if only new list remains...
		{
			addToList (olditer, resultHead, resultTail);
			olditer = olditer -> next; // step through old list
		}
		else if (!newiter) // if only old list remains...
		{
			addToList (newiter, resultHead, resultTail);
			newiter = newiter -> next; // step through new list
		}
		else if ((*olditer) < (*newiter)) // if old list is behind new one...
		{
			addToList (olditer, resultHead, resultTail);
			olditer = olditer -> next; // step through old list
		}
		else if ((*newiter) < (*olditer)) // if new list is behind old one...
		{
			addToList (newiter, resultHead, resultTail);
			newiter = newiter -> next; // step through new list
		}
		else // iterators point to equal items
		{
			addToList (newiter, resultHead, resultTail); // we want the new money value
			olditer = olditer -> next; // step through old list
			newiter = newiter -> next; // step through new list
		}
	}

	return (resultHead);
} // merge

4. Algorithms for sorting

10 pts: Examine the following sequence of ranges that gradually become sorted, mention all sorting algorithms (out of selection sort, bubble sort, insertion sort, shaker sort, and merge sort) that are consistent with this sequence. Justify your answer.

4,0,9,2,3,6,7,1,8,5
4,9,2,3,6,7,1,8,5,0
9,4,3,6,7,2,8,5,1,0
9,4,6,7,3,8,5,2,1,0
9,6,7,4,8,5,3,2,1,0
9,7,6,8,5,4,3,2,1,0
9,7,8,6,5,4,3,2,1,0
9,8,7,6,5,4,3,2,1,0

Can't be merge sort, takes too long.
Can't be selection or insertion as 9 and 4 swap places in line 3.
Can't be shaker as 8 isn't in place until the end.

Is bubble sort.  Next smallest is always in place at end of the pass.  Large
values always move exactly 1 spot to their left each pass.

15 pts: Write a program that will do selection sort and prove its worst-case and best-case big-theta complexity (without referring to Chapter 6 in Sedgewick). Show best-case and worst-case inputs.
```
selection(Item a[], int l, int r)
  { for (int i = l; i < r; i++)
      { int min = i;
        for (int j = i+1; j <= r; j++) 
            if (a[j] < a[min]) min = j;
        exch(a[i], a[min]);
      } 
   }
```
Both best and worse case are big-Theta(N²). The outer for loop runs through every itelm in the array. The inner for loop runs though half of the items in the array on average. This is big-Theta(N²).
The best and worse case are more-or-less the same, both do exactly the same number of comparisions. However a sorted list will do no actual swaps and the condidtion of the if statement will ever be executed, a slight savings. By the same arguement having a reverse-sorted list would provide the maximum number of swaps possible.